Rows: 14,824
Columns: 1
$ base_pay <dbl> 119321.60, 113270.70, 148116.00, 78676.87, 109373.63, 95001.7…Introduction to Frequentist Inference
Bayesian
P (Hypotheses | Data) Hypotheses have probabilities in light of the observed data
Frequentist
P (Data | Hypotheses)
Data have probability considering the conditions of the hypotheses
Credible Intervals
Confidence Intervals
Hypotheses Testing
Notation
| Sample Statistic | Population Parameter | |
|---|---|---|
| Mean | x̄ | μ |
| Standard Deviation | s | σ |
| Variance | s2 | σ2 |
| Proportion | p | π |
Research Question
Are there any pink cows in the world?
Hypotheses
Null hypothesis: There are no pink cows in the world.
Alternative hypothesis: There is a pink cow in the world.
Hypothesis Testing Procedure
We go looking for evidence against the null.
If we find any evidence against the null (a single pink cow) then we can conclude the null is false. We say we reject the null hypothesis.
If we do not find any evidence against the null (a single pink cow) then we fail to reject the null. We can keep searching for more evidence against the null (i.e. continue looking for a pink cow). We will never be able to say the null is true so we never accept the null. All we can do is keep looking for a pink cow.
Research Question
Are there any black cows in the world?
Hypotheses
Null hypothesis: There are no black cows in the world.
Alternative hypothesis: There is a black cow in the world.

When we see a black cow, we reject the null hypothesis and conclude that there is a black cow in the world.
Research Question
Is there a foreign object in the cat’s body?
Hypothesis Testing
Null hypothesis: There is no foreign object in the cat’s body.
Alternative hypothesis: There is a foreign object in the cat’s body.
Collect Evidence
X-ray
Conclusion and Decision
X-ray does not show any foreign object.
- Fail to reject the null hypothesis.
- We cannot conclude the null hypothesis is true. We cannot accept the null hypothesis.
Example
Null hypothesis: There is no problem with my cell phone.
Alternative hypothesis: There is a problem with my cell phone.
Collect Evidence
- Check if the screen is broken.
- Check if the battery life is too short.
- Check if the response times of apps are long.
- …
Conclusion and Decision
No problems were detected.
- Fail to reject the null hypothesis.
- You cannot conclude that there is no problem with the cell phone.
- You can state that there were no problems detected (i.e. there was no evidence against the null).
Remember
- Null hypothesis is always about nothing: no pink cow, no effect, no difference etc.
- We never accept the null hypothesis. We either reject it or fail to reject it.
- In frequentist statistics, we always start hypotheses testing with the assumption that the null hypothesis is true and try to find evidence against it.
Writing Hypotheses with Notation
If there was no variance there would be no need for statistics.
What if?
We want to understand average number of sleep Irvine residents get. What if everyone in Irvine slept 8 hours every night? (
sleep= {8, 8,…, 8})We want to predict who will graduate college. What if everyone graduated college? (
graduate= {TRUE, TRUE,…, TRUE})
We want to understand if Android users spend more time on their phones when compared to iOS users. What if everyone spent 3 hours per day on their phones? (
time= {3, 3,…, 3},os= {Android, Android, …. iOS})We want to understand, if birth height and weight are positively associated in babies. What if every baby was 7.5 lbs? (
weight= {7.5, 7.5,…, 7.5},height= {20, 22,…, 18})
In all these fake scenarios there would be no variance in sleep, graduate, time, weight. These variables would all be constants thus would not even be a variable.
Things vary. We use statistics in research studies to understand how variables vary and often we want to know how they covary with other variables.
To make the connection between research questions of studies and statistics, we will take small steps and begin with writing hypotheses using notation.
Research Question Do UCI students sleep on average 8 hours on a typical night?
Variable sleep (8,7,9,7.5, …)
Research Question Using Notation \(\mu \stackrel{?}{=} 8\)
Hypotheses
\(H_0 : \mu = 8\)
\(H_A : \mu \neq 8\)
\(H_0 : \mu - 8 = 0\)
\(H_A : \mu - 8 \neq 0\)
The parameter we want to infer about is a single mean.
Tip
If you want to type math notation correctly on Gradescope or Quarto out correctly as \(\mu\) then you can write
The double dollar signs at the beginning and at the end let Gradescope know that you are writing a math equation.
Research Question Do the majority of Americans approve allowing DACA immigrants to become citizens?
Variable approve (yes, yes, yes, no, yes, no, no)
Research Question Using Notation \(\pi \stackrel{?}{>} 0.5\)
Hypotheses
\(H_0: \pi < 0.5\)
\(H_A: \pi \geq 0.5\)
The parameter we want to infer about is a single proportion.
Research Question Is California March 2020 unemployment rate different than US March 2020 unemployment rate which is at 4.4%?
Variable unemployed_CA (no, no, yes, no, yes, no, no…)
Research Question Using Notation \(\pi \stackrel{?}{=} 0.044\)
Hypotheses
\[H_0:\pi= 0.044\] \[H_A: \pi \neq 0.044\]
The parameter we want to infer about is a single proportion.
Research Question Are there more STEM majors at UCI than non-STEM majors?
Variable STEM (TRUE, FALSE, FALSE, TRUE, FALSE, TRUE, TRUE…)
Research Question Using Notation \(\pi_{STEM} \stackrel{?}{>} 0.5\)
Hypotheses
\[H_0: \pi \leq 0.5\] \[H_A: \pi > 0.5\]
The parameter we want to infer about is a single proportion.
RQ Do STEM (s) majors have higher or lower (different) income after graduation when compared to non-STEM (n) majors?
Variables explanatory: STEM (TRUE, FALSE, FALSE, TRUE,…)
response: income(40000, 20000, 65490, 115000,…)
Research Question Using Notation \(\mu_{s} \stackrel{?}{=} \mu_{n}\) or \(\mu_{s} - \mu_{n} \stackrel{?}{=}0\)
Hypotheses
\[H_0:\mu_{s} = \mu_{n}\] \[H_A:\mu_{s} \neq \mu_{n}\]
\[H_0:\mu_{s} - \mu_{n} = 0\] \[H_A:\mu_{s} - \mu_{n} \neq 0\]
We want to infer about difference of two means.
RQ Do Democrats and Republicans approve legal abortion at same rates?
Variables explanatory: party (D, D, R, R,…)
response: approve(TRUE, FALSE, FALSE, TRUE,…)
Research Question Using Notation \(\pi_{d} \stackrel{?}{=} \pi_{r}\) or \(\pi_{d} - \pi_{r} \stackrel{?}{=}0\)
Hypotheses
\(H_0:\pi_{d} = \pi_{r}\)
\(H_A:\pi_{d} \neq \pi_{r}\) . . .
We want to infer about difference of two proportions.
| Parameter of Interest | Response | Explanatory | |
|---|---|---|---|
| Single Mean | \(\mu\) | Numeric | |
| Difference of Two Means | \(\mu_1 - \mu_2\) | Numeric | Binary |
| Single Proportion | \(\pi\) | Binary | |
| Difference of Two Proportions | \(\pi_1 - \pi_2\) | Binary | Binary |
A categorical variable with two levels is called a binary variable.
Later on we will also learn
| Parameter of Interest | Response | Explanatory |
|---|---|---|
| \(\beta_1\) | Numeric | Categorical and/or Numeric |
Central Limit Theorem
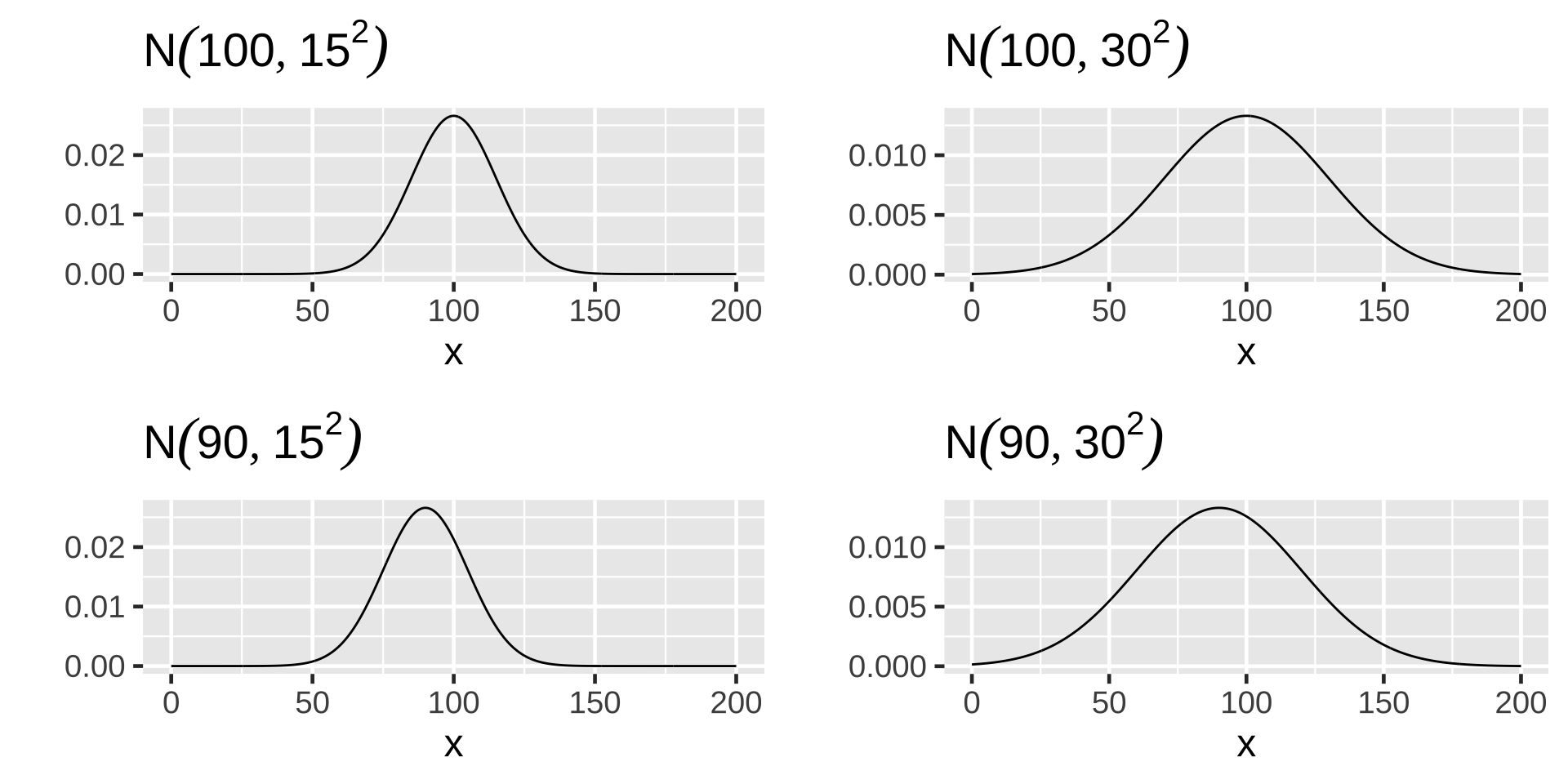
Parameters of a normal distribution \(N(\mu, \sigma^2)\)
Data
We will be using payroll data from Los Angeles Police Department (LAPD) from 2018.
Population Distribution

Population Mean
We have data on everyone who worked for LAPD in the year 2018. So the distribution we just looked at is a population distribution. We can go ahead and calculate the population mean ( \(\mu\) ).
# A tibble: 1 × 1
`mean(base_pay)`
<dbl>
1 85149.Population Standard Deviation
We can calculate the population standard deviation ( \(\sigma\) ).
# A tibble: 1 × 1
`sd(base_pay)`
<dbl>
1 38423.What if we did not have access to all this data? What would we do?
Rely on a sample!
Let’s assume we went ahead and took a (random) sample of LAPD staff and asked their salary information (and they report to us truthfully) and calculated a mean, would we find a mean of 85149.05? Why, why not?
Let’s pretend we have never seen the data and we do not know the population parameter \(\mu\). In fact this is usually what happens in real life. We do not have the population information but we do want to know a population parameter (does not necessarily have to be the mean).
. . . If we took a sample and calculated the sample mean, we would name this point estimate of the parameter.
| Parameter of Interest | Point Estimate / Sample Statistic | |
|---|---|---|
| Mean | \(\mu\) | \(\bar x\) |
| Difference of Two Means | \(\mu_1 - \mu_2\) | \(\bar x_1 - \bar x_2\) |
| Proportion | \(\pi\) | \(p\) |
| Difference of Two Proportions | \(\pi_1 - \pi_2\) | \(p_1 - p_2\) |
First Sample
We would like to know about \(\mu\) but we cannot access the whole population.
A researcher takes a random sample of 20 LAPD staff and ask them about their base pay.
[1] 0.00 109368.20 95924.46 29417.88 32236.80 98306.29 0.00
[8] 95877.27 0.00 61521.20 109054.97 53726.44 89835.29 0.00
[15] 109378.40 69640.00 43810.12 109409.10 103408.00 3600.00Mean of first sample, \(\bar x_1\) =
[1] 60725.72Mean of second sample
\(\bar x_2\) =
[1] 81837.23Mean of third sample
\(\bar x_3\) =
[1] 85614.37We could do this over and over again. Don’t you worry! I did it.
I have taken 10,000 samples of size 200 (sample size of 20 is just too small) and calculated their mean. The following slide shows the distribution of the sample means.
Sampling Distribution of the Mean

Sampling Distribution of the Mean

When certain conditions are met then:
\[\bar x \sim \text{approximately }N( \mu, \frac{\sigma^2}{n})\]
\[(\bar x_1 - \bar x_2) \sim \text{approximately } N(\mu_1 - \mu_2, \frac{\sigma_1^2}{n_1}+ \frac{\sigma_2^2}{n_2})\]
\[p \sim \text{approximately } N(\pi, \frac{\pi(1-\pi)}{n})\]
\[(p_1 - p_2) \sim \text{approximately } N((\pi_1 - \pi_2), {\frac{\pi_1(1-\pi_1)}{n_1} + \frac{\pi_2(1-\pi_2)}{n_2}})\]
Central Limit Theorem (CLT)
If certain conditions are met, the sampling distribution will be normally distributed with a mean equal to the population parameter. The standard deviation will be inversely proportional to the square root of the sample size.
We will learn the conditions in the upcoming lectures.
Moving forward we will use CLT to make inference about population parameters using sample statistics.
Take-Away Messages
- Sample statistics are point estimates. They are not the same thing as population parameters.
- Point estimates can vary from sample to sample. Sampling distribution captures this variance.
