Introduction to Bayesian Inference:
The Beta-Binomial Model
Examples from this lecture are mainly taken from the Bayes Rules! book and the new functions are from the bayesrules package.
Statistical Inference
Making meaning of data
In the first half of the quarter, we retrieved data (by downloading or scraping), opened data, joined data, wrangled data, described data.
In the second half of the quarter we will make meaning of data using statistical inference and modeling.
Research question
Every research project aims to answer a research question (or multiple questions).
Example
Do UCI students who exercise regularly have higher GPA?
Population
Each research question aims to examine a population.
Example
Population for this research question is UCI students.
Sampling
A population is a collection of elements which the research question aims to study. However it is often costly and sometimes impossible to study the whole population. Often a subset of the population is selected to be studied. Sample is the subset of the population that is studied.
Example
Since it would be almost impossible to study ALL UCI students, we can study a sample of students.
Note
The goal is to have a sample that is representative of the population so that the findings of the study can generalize to the population.
Descriptive Statistics vs. Inferential Statistics
In descriptive statistics, we use sample statistics such as the sample mean or proportion to understand the observed data.
In inferential statistics we use the observed data to make an inference about the **population parameters* using probabilistic models.
Bayesian vs. Frequentist Statistics
- These are two major paradigms that define probability and thus two major paradigms to making statistical inference.
- We will make statistical inference using Bayesian methods and next week we will use frequentist methods. Both these methods are valid and used in research.
- Which of these methods you will choose to utilize in your final projects will depend on your understanding of your research topic, your philosophical approach to science, and a few statistical considerations.
Bayesian Inference
Bechdel Test
Alison Bechdel’s 1985 comic Dykes to Watch Out For has a strip called The Rule where a person states that they only go to a movie if it satisfies the following three rules:
the movie has to have at least two women in it;
these two women talk to each other; and
they talk about something besides a man.
This test is used for assessing movies in terms of representation of women. Even though there are three criteria, a movie either fails or passes the Bechdel test.
Let \(\pi\) be the the proportion of movies that pass the Bechdel test.
The Beta distribution is a good fit for modeling our prior understanding about \(\pi\).
We will utilize functions from library(bayesrules) to examine different people’s prior understanding of \(\pi\) and build our own.
The Optimist
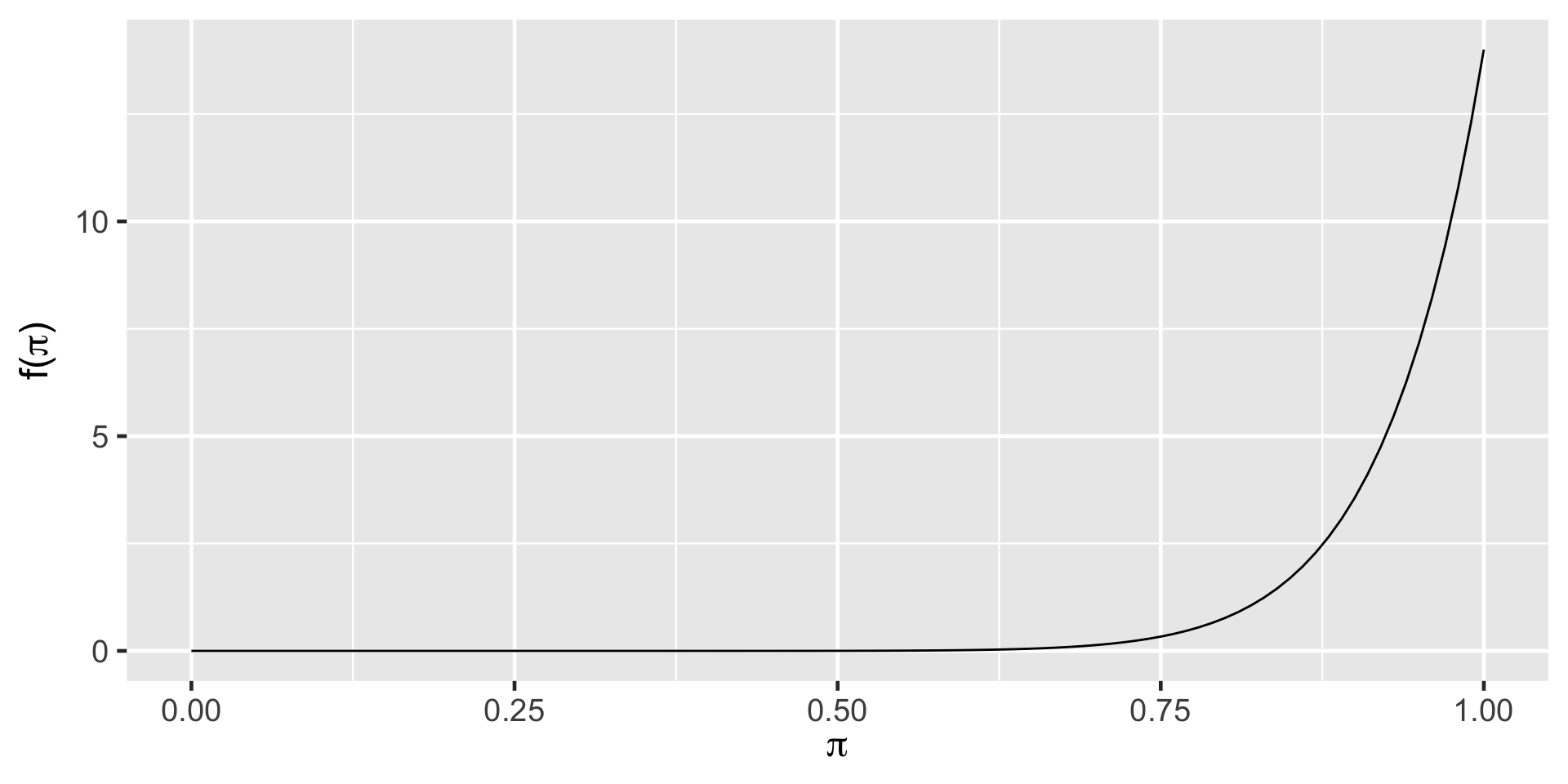
The Clueless

The Feminist

Vocabulary
Informative prior: An informative prior reflects specific information about the unknown variable with high certainty (ie. low variability).
Vague (diffuse) prior:
A vague or diffuse prior reflects little specific information about the unknown variable. A flat prior, which assigns equal prior plausibility to all possible values of the variable, is a special case.
Quiz question
Which of these people are more certain (i.e. have a highly informative prior)?
- The optimist
- The clueless
- The feminist
Plotting Beta Prior

Your prior
What is your prior model of \(\pi\)?
Utilize the summarize_beta() and plot_beta() functions to describe your own prior model of \(\pi\). Make sure to note this down. We will keep referring to this quite a lot.
Data
We are taking a random sample of size 20 from the bechdel data frame using the sample_n() function.
The set.seed() makes sure that we end up with the same set of 20 movies when we run the code. This will hold true for anyone in the class. So we can all reproduce each other’s analyses, if we wanted to. The number 84735 has no significance other than that it closely resembles BAYES.
Data
Rows: 20
Columns: 3
$ year <dbl> 2005, 1983, 2013, 2001, 2010, 1997, 2010, 2009, 1998, 2007, 201…
$ title <chr> "King Kong", "Flashdance", "The Purge", "American Outlaws", "Se…
$ binary <chr> "FAIL", "PASS", "FAIL", "FAIL", "PASS", "FAIL", "FAIL", "PASS",…The Optimist
The Optimist

The Clueless
The Clueless

The Feminist
The Feminist

Comparison

Your Posterior
Utilize summarize_beta_binomial() and plot_beta_binomial() functions to examine your own posterior model.
Balancing Act of Bayesian Analysis

In Bayesian methodology, the prior model and the data both contribute to our posterior model.
Different Data, Different Posteriors
Morteza, Nadide, and Ursula – all share the optimistic Beta(14,1) prior for \(\pi\) but each have access to different data. Morteza reviews movies from 1991. Nadide reviews movies from 2000 and Ursula reviews movies from 2013. How will the posterior distribution for each differ?
Morteza’s analysis
# A tibble: 2 × 2
binary n
<chr> <int>
1 FAIL 7
2 PASS 6[1] 0.4615385Morteza’s analysis

Nadide’s analysis
# A tibble: 2 × 2
binary n
<chr> <int>
1 FAIL 34
2 PASS 29[1] 0.4603175Nadide’s analysis

Ursula’s analysis
# A tibble: 2 × 2
binary n
<chr> <int>
1 FAIL 53
2 PASS 46[1] 0.4646465Ursula’s analysis

Summary

priors: Beta(14,1), Beta(5,11), Beta(1,1)
